This AI Paper Introduces Diffusion Evolution: A Novel AI Approach to Evolutionary Computation Combining Diffusion Models and Evolutionary Algorithms

Artificial intelligence has significantly advanced by integrating biological principles, such as evolution, into machine learning models. Evolutionary algorithms, inspired by natural selection and genetic mutation, are commonly used to optimize complex systems. These algorithms refine populations of potential solutions over generations based on fitness, leading to efficient adaptation in challenging environments. Similarly, diffusion models in AI work by progressively denoising noisy input data to achieve structured outputs. These models iteratively improve initial noisy data points, guiding them toward more coherent results that match the training data distribution. Combining these two domains has the potential to produce novel methods that utilize the strengths of both approaches, thereby enhancing their effectiveness.

One of the primary challenges in evolutionary computation is its tendency to converge prematurely on single solutions in complex, high-dimensional spaces. Traditional evolutionary algorithms such as Covariance Matrix Adaptation Evolution Strategy (CMA-ES) and Parameter-Exploring Policy Gradients (PEPG) effectively optimize simpler problems but tend to get trapped in local optima when applied to more complex scenarios. This limitation makes it difficult for these algorithms to explore diverse potential solutions. As a result, they often fail to maintain the diversity needed to solve multi-modal optimization tasks effectively, highlighting the need for more advanced methods capable of balancing exploration and exploitation.

Traditional evolutionary methods like CMA-ES and PEPG use selection, crossover, and mutation processes to enhance the population’s fitness over successive generations. However, these algorithms need help to perform efficiently when faced with high-dimensional or multi-modal fitness landscapes. For instance, CMA-ES is prone to converge on a single solution even when multiple high-fitness regions are in the search space. This limitation is largely due to its inability to maintain solution diversity, making it challenging to adapt to complex optimization problems with many possible solutions. To overcome these limitations, there is a need for more flexible and robust evolutionary algorithms that can handle complex and diverse optimization tasks.

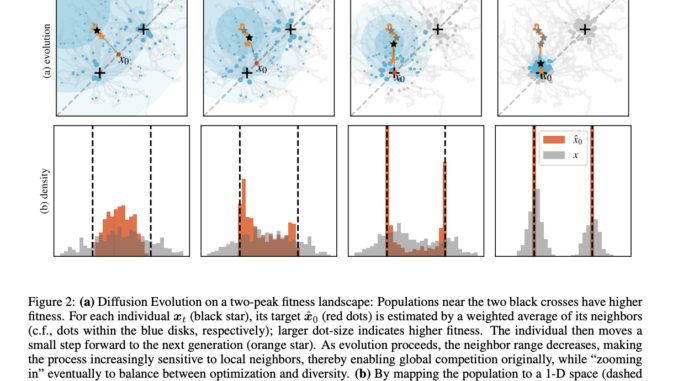
Researchers from the Allen Discovery Center at Tufts University, the Institute for Theoretical Physics at TU Wien, and the Wyss Institute at Harvard University introduced a novel approach called Diffusion Evolution. This algorithm merges evolutionary principles with diffusion models by treating evolution as a denoising process. The research team demonstrated that the algorithm could incorporate evolutionary concepts like natural selection, mutation, and reproductive isolation. Building on this idea, the team introduced the Latent Space Diffusion Evolution method, which reduces computational costs by mapping high-dimensional parameter spaces into lower-dimensional latent spaces. This process allows for more efficient searches while maintaining the ability to find diverse and optimal solutions across complex fitness landscapes.

The Diffusion Evolution algorithm uniquely integrates the iterative denoising steps of diffusion models with natural selection processes. By mapping high-dimensional parameter spaces into lower-dimensional latent spaces, the method performs more efficient searches, identifying multiple diverse solutions within the same search space. This approach enhances the algorithm’s robustness, making it suitable for addressing various optimization challenges. Using latent space diffusion helps overcome traditional methods’ slow convergence and local optima issues, leading to faster convergence and greater solution diversity. This methodology allows the algorithm to maintain flexibility in exploring complex search spaces without compromising performance.

In a series of experiments, the researchers compared Diffusion Evolution with other prominent evolutionary algorithms like CMA-ES, OpenES, and PEPG using several benchmark functions: Rosenbrock, Beale, Himmelblau, Ackley, and Rastrigin. On functions like Himmelblau and Rastrigin, which have multiple optimal points, Diffusion Evolution demonstrated its capability to find diverse solutions while maintaining high fitness scores. For example, on the Ackley function, Diffusion Evolution achieved an average entropy of 2.49 with a fitness score of 1.00, outperforming CMA-ES, which achieved a higher entropy of 3.96 but with lower fitness scores, indicating it was distracted by multiple high-fitness peaks. Furthermore, the experiments demonstrated that Diffusion Evolution required fewer iterations to achieve optimal solutions than CMA-ES and PEPG. For instance, Latent Space Diffusion Evolution reduced the computational steps significantly in high-dimensional spaces, handling tasks with up to 17,410 parameters effectively.

In reinforcement learning tasks, such as balancing a cart-pole system, the Diffusion Evolution algorithm showed promising results. The system consists of a cart with a pole hinged to it, and the objective is to keep the pole vertical as long as possible by moving the cart left or right based on inputs like position and velocity. The research team used a two-layer neural network with 58 parameters to control the cart, and the algorithm achieved a cumulative reward of 500 consistently, indicating successful performance. This demonstrates that Diffusion Evolution can effectively handle complex reinforcement learning environments, highlighting its practical applications in real-world scenarios.

In conclusion, the Diffusion Evolution algorithm significantly advances evolutionary computation by integrating diffusion models’ strengths. This approach improves the ability to maintain solution diversity and enhances overall problem-solving capabilities in complex optimization tasks. By introducing Latent Space Diffusion Evolution, the researchers provided a robust framework capable of solving high-dimensional problems with reduced computational costs. The algorithm’s success in diverse benchmark functions and reinforcement learning tasks indicates its potential to revolutionize evolutionary computation in AI and beyond.

Check out the Paper. All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on Twitter and join our Telegram Channel and LinkedIn Group. If you like our work, you will love our newsletter.. Don’t Forget to join our 50k+ ML SubReddit

[Upcoming Event- Oct 17 202] RetrieveX – The GenAI Data Retrieval Conference (Promoted)